16議事録 (いちろくぎじろく)

プリン分割問題に終止符。

この問題とは、大きなカップ入りプリンを半分こするには
どのくらい残せば良いか（どのくらい食べて良いか）を考察したものである――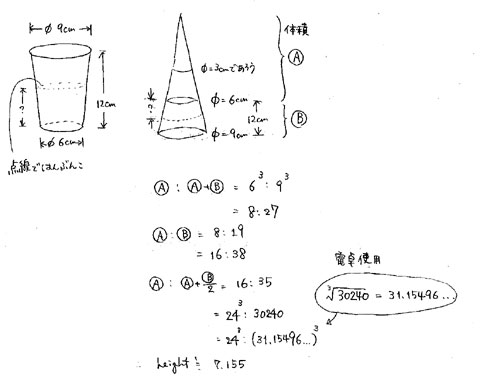



画像左上の図をご覧ください。
上底面は直径9cm、下底面は直径6cmのそれぞれ円、高さ12cmであると計測されました。
ここから、図に書き込まれた「？」を求めようというわけです。
（高さの12cmが側面に沿って計測された可能性もありますが、解には影響しないので別段考えない）

3次というあまりの計算の面倒さにその場では「7.2cm」と口頭で答えたものの
（「7.2cm」の根拠は、12cmをとりあえず 9:6 に内分したことから）
真面目に計算せずに済ませてしまったのが少々もったいないので、ここで最後まで解いておきます。


画像に全部書き込んじゃいましたが、改めて説明すると
この計算で「円周率」を出してくるやつはアホです。（ｷﾘｯ

プリンの形（円錐台）をひっくり返して、側面を延長して大円錐を作り、
仮想部分（小円錐）をＡ、実部分（円錐台）をＢとします。
図中ではＡ,Ｂの体積をそれぞれマルＡ,マルＢと書いていますがここではそのままA,Bと書きます。
　↓
A : A+B = 6^3 : 9^3 = 8 : 27 (小円錐と大円錐は相似)
A : A+B/2 = 16 : 35 (A+B/2は、半分になったプリンに仮想部分を加えたもの)
　　　　 = 24^3 : 30240 (円錐の高さの相似比が知りたい)

30240の3乗根なんて計算できない、開立なんて知らないから
10^3だけ外に出して、電卓で近似計算しながら求めていきます。
[３][．][１][１][×][×][＝][＝]　→　30.080231
[３][．][１][２][×][×][＝][＝]　→　30.371328
とかやりながら。

これによって 30240の3乗根が概ね31.155と判りました。
求めるべき高さは、これから仮想部分の高さ24を引いて 約7.155(cm)。

だいたい合ってた

--------------------------------------------------

こんな計算をしてみるのもたまには良いんですけど
7.155cmだからといって正確に食べ残すのは困難だし
どれだけ意義があったのかというとねえ……