16議事録 (いちろくぎじろく)

iアプリ「Magical Emulator」開発の上で一番の難所を超えた所なので、
QMAのキューブクイズみたいなものを作りたい方へのヒントも込めて解説をいたします。

まずは完成品（見本）がこれ。理由あり画質。
画像は静止画ですがちゃんと回転します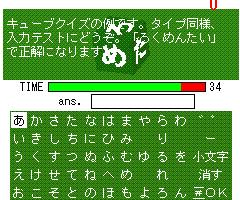


これは、緑地に白文字を書いた40×40ピクセルの画像6枚から成ってます。
うち3枚は裏側に回ってるため描画してません。
描画の際には、Graphics#drawImage のアフィン変換を使って各画像を平行四辺形に変換してます。

さて、そのアフィン変換行列の求め方の話をば。

まず、普通に画像を描画すると
左上(0,0) 右下(40,40) となります。下方向がy軸正の向きであることに注意。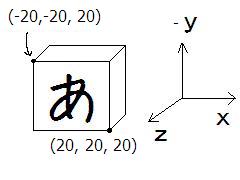



[1]
これを画像の「あ」面に移す変換はというと、単なる平行移動ですから
A = {{1,0,0,-20}{0,1,0,-20}{0,0,1,20}{0,0,0,1}}。
ただし、空間上の点は縦行列
t{x,y,z,1}={{x}{y}{z}{1}}
で表すものとします。4行目の「1」は固定


[2]
「あ」面を左右の側面に移す変換は、y軸を回転軸にして90度回せばよいので
{{0,0,1,0}{0,1,0,0}{-1,0,0,0}{0,0,0,1}}と
{{0,0,-1,0}{0,1,0,0}{1,0,0,0}{0,0,0,1}}
となります。
「あ」面を上下の底面に移す変換は、x軸を回転軸にして90度回せばよいので
{{1,0,0,0}{0,0,1,0}{0,-1,0,0}{0,0,0,1}}と
{{1,0,0,0}{0,0,-1,0}{0,1,0,0}{0,0,0,1}}
となります。
「あ」面を背面に移す変換は、x軸y軸どっちでもよいので(字の向きが変わるだけ)180度回転。
{{-1,0,0,0}{0,1,0,0}{0,0,-1,0}{0,0,0,1}}または
{{1,0,0,0}{0,-1,0,0}{0,0,-1,0}{0,0,0,1}}
のどちらか。マイナスを奇数個つけると鏡像になるので注意。
あとついでに「あ」面を「あ」面に移すid(行列は単位行列)。

これらをTとします。


[3]
キューブの回転は
「x軸を中心に角度γだけ回転」
{{1,0,0,0}{0,cosγ,-sinγ,0}{0,sinγ,cosγ,0}{0,0,0,1}}
「y軸でβ回転」
{{cosβ,0,-sinβ,0}{0,1,0,0}{sinβ,0,cosβ,0}{0,0,0,1}}
「z軸でα回転」
{{cosα,-sinα,0,0}{sinα,cosα,0,0}{0,0,1,0}{0,0,0,1}}
これらを順に左に作用させて、
R(α,β,γ) = {{cosαcosβ,-sinαcosγ-cosαsinβsinγ,sinαsinγ-cosαsinβcosγ,0}{sinαcosβ,cosαcosγ-sinαsinβsinγ,-cosαsinγ-sinαsinβcosγ,0}{sinβ,cosβsinγ,cosβcosγ,0}{0,0,0,1}}

※ここで行列式(detR)が1になることを確認。α,β,γは適当に決めないと計算やってらんない


以上[1][2][3]から、アフィン変換行列は
R(α,β,γ)×T(6通り)×A
から求められます。
とても面倒でここに書く気は起こりませんが、一応これで回るキューブが描画できてるので大丈夫なはず。

凸多面体なので、描画/非描画の判定には
「面の中心を移した先のz座標が正であるか」を見ればよい。


こんな工夫があってキューブは完成したわけです。
マスコットカプセルじゃ表面の文字が変えられないと思うので。

ほぼ同じ考え方で四面体・八面体も作れますね。
ただし面が正三角形なので工夫が求められますが。

と、いうことで。
キューブクイズみたいな物を作りたいという方がいらっしゃいましたら参考にしてください。
3Dモデルの表面の文字が変えられるのなら、そっちを使ったほうが断然お得ですが。